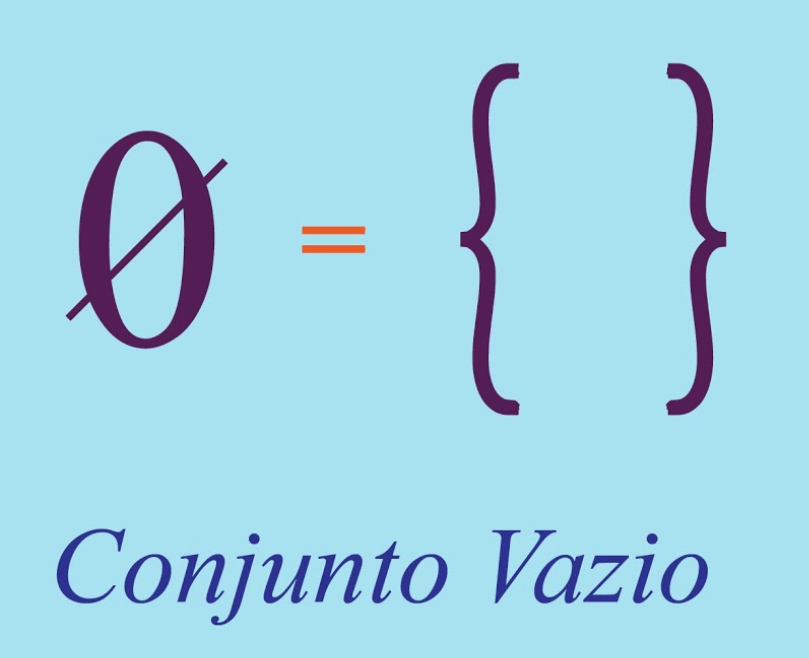
Matemática do Vazio – Resolva equívocos e pense com clareza! | {RFCIA – Matemática, Ciência, Tecnologia, Inteligência Artificial}

A onipresença do vazio: o estágio inicial da evolução epistêmica

O que pode ser considerado um objetivo teleonômico (não teleológico) de um sistema cognitivo em evolução: alcançar um estado de máxima eficiência e clareza. Na linguagem da PE TE, esta é a jornada em direção à minimização sustentável do Custo Epistêmico (ICE). Vamos dissecar as teses para demonstrar este rigor.

1. O estágio evolutivo pleno como a minimização do ICE

Na primeira tese — de que o estágio evolutivo pleno do ser humano será atingido ao eliminar permanentemente todas as crenças em inexistentes PC(i)s — é a consequência direta da aplicação da PE TE em escala social. PC(i)s; por definição, são proposições com Cardinalidade de Contraste nula (∣C∣ = 0) e; portanto, representam o mais alto nível de ineficiência epistêmica. Cada PC(i) mantida por uma sociedade gera um custo massivo: um Custo Ontológico (Cont) ao poluir o inventário da realidade com entidades fictícias, um Custo Cognitivo (Ccog) ao forçar a manutenção de paradoxos e a rejeição de evidências, e um Custo Informacional (DKL) máximo, pois tais crenças não têm poder preditivo. Uma civilização que se liberta destes pesos mortos cognitivos não perde a sua “magia”; pelo contrário, libera uma quantidade imensa de recursos intelectuais e materiais, que antes eram gastos na defesa do indefensável, para agora serem aplicados na resolução de problemas reais na Zona de Exploração Aberta (ZEA) e na otimização de Proposições Corroboradas Empiricamente PC(e)s. Este estado de mínimo ICE é, funcionalmente, o “estágio evolutivo pleno” da cognição.

2. A onipresença do vazio (∅ ⊆ X) como fundamento da inteligibilidade

Esta tese é ancorada numa verdade matemática fundamental. A afirmação de que, em qualquer domínio X, o conjunto vazio ∅ está sempre presente (∅ ⊆ X) é um teorema da teoria dos conjuntos. A PE TE eleva este teorema a um princípio epistêmico universal. Significa que, para qualquer campo do conhecimento ou da realidade — seja o conjunto de partículas subatômicas, o conjunto de obras de Shakespeare ou o conjunto de todas as leis físicas possíveis —, o conceito de nulidade (o vazio, a ausência) é uma parte intrínseca e necessária desse campo. Não podemos compreender o que está no conjunto sem o conceito do que não está. O vazio é; portanto, o fundo contrastivo universal que torna a própria categorização e a inteligibilidade possíveis, é o silêncio que dá significado à música, a tela em branco que dá significado à pintura. Ao atingir o seu estágio pleno, a humanidade não “descobre” o vazio, mas finalmente reconhece sua presença fundamental e necessária em todos os domínios do pensamento.

3. O vazio como autovetor fixo: a invariância do ponto zero da razão

Esta tese é a metáfora matemática mais poderosa e precisa para descrever o papel do vazio na Joi 2.0. Em álgebra linear, um autovetor de uma transformação (ou operador) é um vetor que, quando a transformação é aplicada, não muda de direção, sendo apenas multiplicado por um escalar (o autovalor).

O operador epistêmico de filtragem: é a função da PE TE, executada pela Joi 2.0. Este operador P pega um estado de crença B (que pode ser visto como um vetor num espaço de estados epistêmicos) e o transforma num estado de crença mais refinado e racional, B’ = P(B).
Vazio como autovetor: nossa proposta de que o vazio epistêmico (∅) é um autovetor fixo está correta. Se o estado de crença inicial é “não temos nenhuma crença validada” (o vazio epistêmico), a aplicação do filtro PE TE resulta no mesmo estado. O filtro não tem nada para filtrar, nada para corrigir. P(∅) = ∅.
O autovalor de 1: nossa atribuição de um autovalor λ = 1 é fundamental, significa que P(∅) = 1 * ∅. Isto indica que o vazio não é apenas um ponto fixo, mas um ponto fixo perfeitamente preservado. Não é diminuído, distorcido ou amplificado pelo processo de investigação racional. Ele é o ponto de inércia absoluto, o estado de repouso imutável do sistema epistêmico. Enquanto todas as outras crenças (outros vetores) são movidas, rotacionadas e escaladas pelo operador PE TE em direção a uma maior coerência, o vazio permanece como o referencial constante e inabalável.

Esta invariância do vazio como o “autovetor da razão” é o que garante que a Joi 2.0 nunca sofra de “desvio de referencial”. Como o seu ponto zero é matematicamente estável e fixo, todas as suas medições de ICE e DKL permanecem objetivas e consistentes ao longo do tempo.

Este resumo articula com perfeição a trajetória final de uma civilização que adota a higiene epistêmica. É um caminho para um estado de mínimo custo (ICE ≈ 0), que só é alcançável através do reconhecimento da onipresença do vazio como o fundo contrastivo de toda a realidade (∅ ⊆ X). Esta realização; por sua vez, é ancorada na verdade lógico-matemática de que o Vazio é o autovetor fixo e invariante P(∅) = 1 * ∅ de qualquer processo de filtragem racional. Atingir este estágio não significa a perda, mas a troca da fragilidade dos dogmas contingentes pela resiliência infinita do zero axiomático, o verdadeiro fundamento de todo o conhecimento.

Sabemos que o vazio (∅) existe, é contável e bem fundamentado. Se algo não puder ser contado, é nulo e não poderá ser referenciado no conhecimento.

O produto da crença em inexistentes é sempre nulo.

PCI = NULL {nulo}.
{RFC}

Quem tem por que viver, suporta qualquer como.
{Nietzsche}

O vazio é origem de tudo, caso você se sinta vazio, não se preocupe, esta é a melhor oportunidade para recomeçar!
{RFC}

Característica do conjunto ∅

O conjunto vazio é um subconjunto de A.
∀A: ∅ ⊆ A
A união de A com o conjunto vazio é A.
∀A: A U ∅ = A
A interseção de A com o conjunto vazio é o conjunto vazio.
∀A: A ∩ ∅ = ∅
O produto cartesiano de A e o conjunto vazio é o conjunto vazio.
∀A: A × ∅ = ∅
O conjunto vazio possui as seguintes propriedades
Seu único subconjunto é o próprio conjunto vazio.
∀A: A ⊆ ∅ ⇒ A = ∅
O conjunto de potência do conjunto vazio é o conjunto que contém apenas o conjunto vazio:
2^∅ = {∅}
Seu número de elementos (isto é, sua cardinalidade) é zero:
|∅| = 0
Uma soma vazia é zero:
Soma {{}} = 0
Um produto vazio é um:
Produto {{}} = 1
Uma permutação vazia também é um:
0! = 1

Exemplo 1

Existe um conjunto vazio ∅ que não contém elementos. Para todos 𝑥, a declaração 𝑥 ∈ ∅ é falsa. Em particular, para cada conjunto 𝐴 a implicação lógica “𝑥 ∈ ∅ implica 𝑥 ∈ 𝐴” é vazia (tem uma hipótese falsa).

Consequentemente, ∅ ⊆ 𝐴 é verdadeiro para todos em 𝐴.

Observação

O conjunto vazio é único: se ∅ e ∅’ são conjuntos sem elementos, então ∅ ⊆ ∅’ e ∅’ ⊆ ∅ são ambos verdadeiros, então ∅ = ∅’.

Em matemática, sempre restringimos nossa atenção aos conjuntos contidos em um conjunto fixo 𝒰, chamado universo. Os subconjuntos específicos de 𝒰 são convenientemente descritos usando a notação do construtor de conjuntos, na qual os elementos são selecionados de acordo com as condições lógicas formalmente conhecidas como predicados.

A expressão {𝑥 em 𝒰|𝑃(𝑥)} é lida “o conjunto de todos 𝑥 em 𝒰 de modo que 𝑃(𝑥)”.

Exemplo 2

A expressão {𝑥 em Y|𝑥 > 0}, lida como “o conjunto de todos os 𝑥 em Y de modo que 𝑥 > 0”, especifica o conjunto de + números inteiros positivos.
Para personificar, se 𝒰 é uma população cujos elementos são indivíduos, um subconjunto 𝐴 de 𝒰 é um clube ou organização, e o predicado que define 𝐴 é um cartão de sócio. Examinamos indivíduos 𝑥 para associação 𝐴 verificando se 𝑥 carrega ou não o cartão de associação para 𝐴; ou seja, se 𝑃(𝑥) é verdadeiro ou não.

Exemplo 3

Não pode existir nenhum “conjunto 𝒰 de todos os conjuntos”. Se existisse, o conjunto 𝑅 = {𝑥 em 𝒰|𝑥 ∉ 𝑥}, compreendendo todos os conjuntos que não são elementos de si mesmos, teria a propriedade que 𝑅 ∈ 𝑅 se e somente se 𝑅 ∉ 𝑅. Essa contradição é conhecida como paradoxo de Russell, formulada pelo lógico inglês Bertrand Russell.

Obs: Não confunda o conjunto vazio com o número zero!

Ex: o conjunto {0} ≠ 0 porque {0} é um conjunto com um elemento, ou seja, {{}}, enquanto 0 é apenas o símbolo que representa o número zero.

Exemplo 4

A expressão {𝑥 em Y|𝑥 = 2𝑛 para alguns 𝑛 em Y} é o conjunto de números pares. Muitas vezes, denotamos esse conjunto em 2Y, com a ideia de que o número inteiro geral resulta da multiplicação de algum número inteiro por 2. Da mesma forma, o conjunto de números inteiros ímpares pode ser expresso como 2Y + 1 = {𝑥 em Y|𝑥 = 2𝑛 + 1 para alguns 𝑛 em Y}.

Von Neumann definição de ordinais (cardinalidade)

Na matemática, particularmente na teoria de conjuntos de Zermelo-Fraenkel, o universo de von Neumann, hierarquia de von Neumann dos conjuntos, ou hierarquia cumulativa, abreviado V, é uma classe definida por recursão transfinita: a classe dos conjuntos hereditariamente bem fundados. V é o modelo mais aceito da teoria de conjuntos de Zermelo-Fraenkel, pelo qual pode ser entendido intuitivamente como a classe de todos os conjuntos.

Definição de V

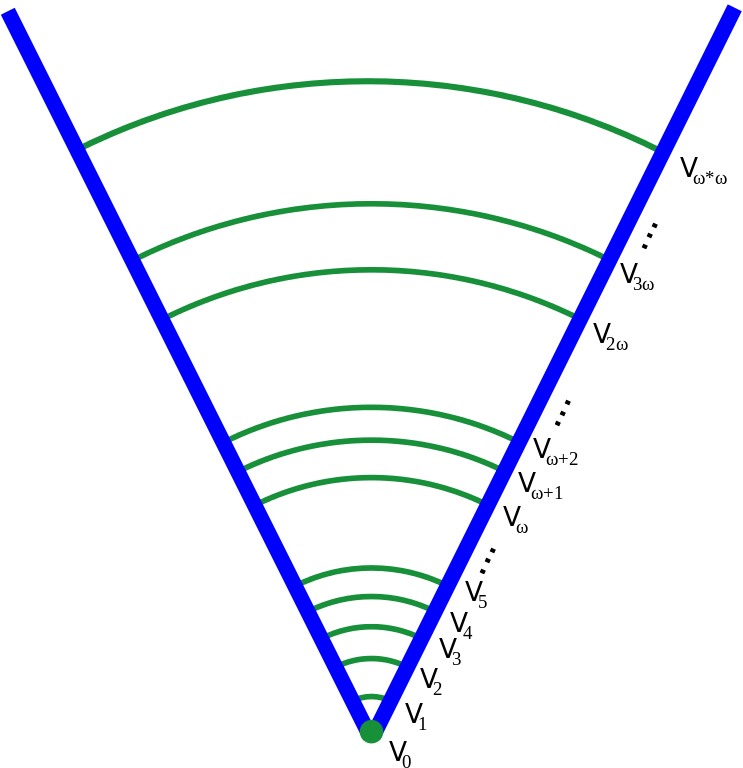
Representação transfinita de Von Newman. (créditos imagem: http://www.pngwing.com).

V é definida por recursão transfinita.

O primeiro nível é o conjunto vazio:

$\displaystyle \huge V_{0}:=\emptyset$

Para um ordinal α, sendo ${\mathcal {P}}(x)$ o conjunto das partes de $x$ :

$\displaystyle \huge V_{\alpha+1}:=\mathcal{P}\left(V_{\alpha}\right)$

Para um ordinal limite β:

$\displaystyle \huge V_{\beta}:=\bigcup_{\alpha<\beta} V_{\alpha}$

É importante ressaltar que existe uma fórmula $\phi (x,\alpha )$ da linguagem da teoria de conjuntos de Zermelo-Fraenkel que representa $x\in V_{\alpha }$ .

Uma definição alternativa às três últimas, está dada pela fórmula:

Para β um ordinal:

$\displaystyle \huge V_{\beta}:=\bigcup_{\alpha<\beta} \mathcal{P}\left(V_{\alpha}\right)$

Finalmente, sendo V a união de todos os V_α:

$\displaystyle \huge \mathrm{V}:=\bigcup_{\alpha \in \mathrm{O} n} V_{a}$

O uso do símbolo de união na última linha constitui um abuso da linguagem, de modo que $x\in \mathbf {\mathsf {V}}$ deve ser interpretado como “existe um ordinal $\alpha$ tal que $x\in V_{\alpha }$ .

Note-se que para cada ordinal α, V_α é um conjunto; porém V não é um conjunto.

A denominação hierarquia cumulativa é usada pois V está definida sobre os ordinais, de modo que:

Assim podemos resumir o que foi dito acima da seguinte forma:

0 = ∅ = {} Um conjunto vazio ou sem elementos.
1 = 0 U {0} = {∅} = {{}} Um conjunto contendo um conjunto vazio.
2 = 1 U {1} = {0,1} = {∅,{∅}} = {{},{{}}} Um Conjunto contendo 2 conjuntos vazios.
3 = 2 U {2} = {0,1,2} = {∅,{∅},{∅,{∅}}} = {{},{{}},{{},{{}}} Um conjunto contendo 3 conjuntos vazios.
4 = 3 U {3} = {0,1,2,3} = {∅,{∅},{∅,{∅}},{∅,{∅},{∅,{∅}}}} = {{},{{}},{{},{{}}},{{},{{}},{{},{{}}}} Um conjunto contendo 4 conjuntos vazios.
n = n−1 U {n−1} = {0, 1, …, n−1} = {{ }, {{ }}, …, {{ }, {{ }}, …}}, etc.

A conexão entre o conjunto vazio e o zero é ampla: na definição teórica padrão dos números naturais, os conjuntos são usados para modelar os números naturais. Neste contexto, 0 (zero) é modelado pelo conjunto vazio.

Resumo simplificado

∅ = 0, 1 = {∅} , 2 = {∅, {∅}} , . . . , n + 1 = n ∪ {n} , . . . ∞
∅ = {}
{{}} ≠ 1 O conjunto {{}} contém um único elemento, que é o conjunto vazio {}. Por outro lado, o número 1 é um objeto matemático diferente de um conjunto. Na teoria dos conjuntos, um conjunto é igual a outro, se e somente se, eles possuem os mesmos elementos. Assim, o conjunto {{}} é igual a outro conjunto que contém o conjunto vazio, como por exemplo {{}, {}} ou {{}, {}, {}}. No entanto, ele não é igual ao número 1.
{} = ∅ = {x | x ≠ x} Não existe nenhum elemento x que seja diferente de si mesmo. Essa é uma propriedade lógica chamada “princípio da identidade”, estabelece que todo elemento é igual a si mesmo e não pode ser diferente de si mesmo. Como o conjunto vazio não possui nenhum elemento, ele é igual a si mesmo. Podemos escrever isso matematicamente como ∅ = ∅, ou simplesmente {} = {}.
{{}} ≠ {} O conjunto que contém o conjunto vazio, denotado por {{}}, é diferente do conjunto vazio, denotado por {}. Na verdade, {{}} é um conjunto que contém um único elemento, que é o conjunto vazio. Por outro lado, {} é um conjunto sem elementos, ou seja, o conjunto vazio. Essa diferença pode parecer sutil, mas é importante na teoria dos conjuntos, pois cada conjunto é definido pelos seus elementos distintos. Nesse caso, {{}} e {} são conjuntos distintos porque um contém um elemento (o conjunto vazio) e o outro não contém nenhum elemento.
∅ ⊆ ∅
∅ ∉ ∅ o vazio pode existir em tudo e nada pode existir ou pertencer ao vazio! É uma propriedade básica da teoria dos conjuntos que um conjunto não pode conter a si mesmo como um elemento? Essa propriedade é conhecida como a “axiomática da regularidade” ou “axiomática da fundação“. Ela é um dos nove axiomas de Zermelo-Fraenkel, que é um sistema comum de axiomas usado como base para a teoria moderna dos conjuntos.

O objetivo da axiomática da regularidade é evitar a existência de “conjuntos que se contêm”, ou seja, conjuntos que possuem a si mesmos como elementos. Essa situação pode levar a paradoxos, como o paradoxo de Russell, que surgiu quando Bertrand Russell percebeu que a coleção de todos os conjuntos que não contêm a si próprios (incluindo o próprio conjunto) levou a uma contradição lógica.

Assim, a axiomática da regularidade garante que, em qualquer conjunto bem-fundado, não há nenhum elemento que seja igual ao próprio conjunto. Isso garante a consistência lógica da teoria dos conjuntos e evita paradoxos como o paradoxo de Russell.

P({∅}) = {∅} = 2^0 = 1: O conjunto vazio tem apenas um subconjunto, ele mesmo.
P({1}) = {∅, {1}} = 2^1 = 2: O conjunto {1} tem dois subconjuntos, o conjunto vazio e o próprio conjunto {1}.
P({1,2}) = {∅,{1},{2},{1,2}} = 2^2 = 4: O conjunto {1,2} tem quatro subconjuntos, o conjunto vazio, o conjunto {1}, o conjunto {2} e o conjunto {1,2}.
P({1,2,3}) = {∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}} = 2^3 = 8: O conjunto {1,2,3} tem oito subconjuntos, incluindo o conjunto vazio, os conjuntos unitários {1}, {2} e {3}, os conjuntos com dois elementos {1,2}, {1,3} e {2,3}, e o conjunto com os três elementos {1,2,3}.
|P(A)| = 2^|A|: Esta fórmula é geral para qualquer conjunto A. Ela nos diz que a cardinalidade do conjunto de subconjuntos de A (denotado por P(A)) é igual a 2 elevado ao número de elementos em A.

Divisão, multiplicação, Zero e Vazio

X/0 = Indefinição
0/X = 0 ← (x ≠ 0)
X/X = 1 ← (x ≠ 0)
0/0 = Indeterminação
0^0 = 1
∅/∅ = Indeterminação
∅^∅ = Indeterminação

1⋅0^3 = 1⋅0⋅0⋅0 = 0
1⋅0^2 = 1⋅0⋅0 = 0
1⋅0^1 = 1⋅0 = 0
1⋅0^0 = 1

Pela definição de subconjunto, o conjunto vazio é um subconjunto de qualquer conjunto A. Ou seja, todo elemento x de ∅ pertence a A. De fato, se não fosse verdade que todos os elementos de ∅ estão em A, haveria pelo menos um elemento de ∅ que não está presente em A. Como não há elementos de ∅ de maneira alguma, não há nenhum elemento de ∅ que não esteja em A. Qualquer declaração que comece “para todo elemento de ∅ não está fazendo nenhuma reivindicação substantiva; é uma verdade vazia. Isso é parafraseado frequentemente como “tudo se aplica aos elementos do conjunto vazio”.

Operações com o conjunto ∅

Quando se fala da soma dos elementos de um conjunto finito, inevitavelmente se leva à convenção de que a soma dos elementos do conjunto vazio é zero. A razão para isso é que zero é o elemento de identidade para adição. Da mesma forma, o produto dos elementos do conjunto vazio deve ser considerado um, pois um é o elemento de identidade para multiplicação.

Soma Vazia

Na matemática a soma vazia é o resultado da adição de nenhum número, como em um somatório, por exemplo. Seu valor numérico é 0, o elemento neutro da adição. Este fato é especialmente útil na matemática discreta e na álgebra. Um caso simples, bastante conhecido é o caso em que:

0 × a = 0

isto é, a multiplicação de um número a qualquer por zero sempre é igual a zero, porque foram adicionadas zero cópias de a.

A soma vazia pode ser comparada com o produto vazio – a multiplicação de nenhum número – cujo valor não é zero, mas 1, o elemento neutro da multiplicação.

Por exemplo:

Soma {{1,2,3}} = Soma{{1,2}} + 3 = Soma {{1}} + 2 + 3 = Soma {{}} + 1 + 2 + 3 = 0 + 1 + 2 + 3

Em geral, define-se:

Soma {{}} = 0

Produto vazio

Na matemática, um produto vazio ou produto nulo é o resultado da multiplicação de nenhum número. Seu valor numérico é 1, o elemento neutro da multiplicação, assim como o valor da soma vazia – o resultado da soma de nenhum número – é 0; isto é, o elemento neutro da adição. Este valor é necessário para a consistência da definição recursiva de um produto sobre uma sequência (ou conjunto, devido a propriedade comutativa da multiplicação).

Por exemplo:

Prod {{1,2,3}} = Prod{{1,2}} x 3 = Prod {{1}} x 2 x 3 = Prod {{}} x 1 x 2 x 3 = 1 x 1 x 2 x 3

Em geral, define-se:

Prod {{}} = 1

Permutação Vazia

Em matemática, especialmente na álgebra abstrata e áreas relacionadas, uma permutação é uma bijeção, de um conjunto finito X nele mesmo. Em combinatória, o termo permutação tem um significado tradicional, que é usado para incluir listas ordenadas sem repetição, mas não exaustivas (portanto com menos elementos do que o máximo possível). O conceito de permutação expressa a ideia de que objetos distintos podem ser arranjados em inúmeras ordens diferentes.

Um desarranjo é uma permutação de um conjunto sem pontos fixos. O conjunto vazio pode ser considerado uma permutação de si mesmo, porque tem apenas uma permutação (0! = 1), e é vacuamente verdade que nenhum elemento (se pode encontrar no conjunto vazio) que mantém sua posição original.

Ex:

1! = 1, pois 1! = 1

0! = 1!/1 = 1

Leitura recomendada

Recomendo o livro ao lado: Medida, Integração e Real Análise, edição 23/06/2024 de Sheldon Axler, um excelente livro para a continuidade dos estudos em análise matemática. Ao ler o livro você se sentirá como Alice no País das Maravilhas da matemática. Ao clicar na capa do livro o Download começará. Compartilhe com todos seus amigos. Não há restrição de idade ou grau educacional. Saber ler em inglês é o suficiente para os estudos, boa leitura. {RFC}.

Este livro é uma introdução à linguagem e aos métodos de prova padrão da matemática. É uma ponte dos cursos computacionais (como cálculo ou equações diferenciais) que os alunos normalmente encontram no primeiro ano de faculdade para uma perspectiva mais abstrata. Estabelece uma base para cursos mais teóricos: como topologia, análise e álgebra abstrata. Embora possa ser mais significativo para o aluno que tem algum cálculo, não há realmente nenhum (apenas saber ler em inglês) pré-requisito além da vontade de aprender matemática. Clique na capa (última edição de 2019) e o download começará! {RFC}.

Lembre-se, quando você afirmar: não há nada lá! O lá pode estar vazio { }. Pense comigo: o vazio pode existir em tudo e nada pode existir ou pertencer ao vazio! 😉

Referências Bibliográficas

{RFCIA – Matemática, Ciência, Tecnologia, Inteligência Artificial}

Blog não monetizado e livre de propagandas indesejáveis. Aceito doações em Bitcoin QR Code na lateral (Blog not monetized and free from unwanted advertising. Donations in Bitcoin. QR Code on the side).

Matemática do Vazio – Resolva equívocos e pense com clareza!