O que são espaços e subespaços matemáticos?

Os espaços/subespaços da matemática são 100% conceituais/abstratos/subjetivos, são invenções cognitivas humanas (porque é nosso cérebro que faz matemática via simulação cerebral e todos os seres que possuem cérebros, ex: aranhas, também realizam procedimentos equivalentes, assim como as abelhas, observe a simetria de suas projeções geométricas) para que a ciência matemática possa existir e possa ser usada em nossas vidas. Experimentos e ferramentas com precisão extrema como as novas fábricas que utilizam EUV (UVE – Ultra Violeta Extrema) para fabricação de chips da TSMC de chips de silício de 3 (nm) nanômetros (previstos para 2023) (1 nm = metro ou 0,000.000.001 metro – um milionésimo de milímetro ou um bilionésimo de metro). O Brasil também está na vanguarda tecnológica com a nossa mais nova fábrica de luz síncroton Sirius (leia abaixo sobre nosso acelerador de luz de 4ª geração.). Também podemos atribuir possibilidades existenciais aos espaços/subespaços matemáticos.

O que são espaços e subespaços físicos?

Os espaços/subespaços da física são a infraestrutura (tecido) do próprio universo (nossos corpos e todas as coisas físicas ocupam espaços físicos), correspondem à realidade objetiva que independe de nossa concepção/abstração, também podemos atribuir possibilidades existenciais a eles.

Podemos ver na foto acima que ambos os tabletes (o Sumério de 6000 anos atrás e os tabletes atuais), ocupam lugares no espaço; entretanto, os tabletes atuais possuem subespaços compactados em seu interior contendo bilhões de componentes nanométricos (chips de silício).

Observatório de Ondas Gravitacionais por Interferômetro Laser

O Observatório de Ondas Gravitacionais por Interferômetro Laser (em inglês: Laser Interferometer Gravitational-Wave Observatory – LIGO). Em 11 de fevereiro de 2016, o projeto LIGO anunciou a detecção de ondas gravitacionais a partir do sinal encontrado às 09h51 UTC de 14 de setembro de 2015, de dois buracos negros com cerca de 30 massas solares em processo de fusão, a 1,2 bilhão de anos-luz da Terra. Isso confirmou a existência de espaços físicos que podem ser dobrados (contraídos pelas ondas gravitacionais). Em 3 de outubro de 2017, o Prêmio Nobel de Física foi atribuído a Rainer Weiss, Barry Barish e Kip Thorne por contribuições decisivas para o detector LIGO e a observação de ondas gravitacionais.

A animação acima mostra a coalescência (junção) de dois buracos negros em órbita, detectados pelos observatórios Ligo e Virgo avançado em 14 de agosto de 2017. A força da onda gravitacional é indicada tanto pela elevação quanto pela cor, com verde escuro indicando fracos campos e violeta brilhante indicando campos fortes. A amplitude da onda gravitacional é redimensionada no tempo, o que permite mostrar o sinal durante toda a coalescência e não apenas perto da fusão, onde é mais forte. Os tamanhos dos buracos negros foram aumentados por um fator de dois para melhorar a visibilidade.

Obs: não é a natureza que faz matemática – nosso universo não é matemático, somos nós por meio de nossa capacidade cognitiva (nosso cérebro) realizamos tal conquista. A natureza/física já nasceu com suas próprias leis que independem de nossa limitação em sua percepção ou compreensão.

{RC}.

A diferença entre espaços/subespaços físicos e matemáticos

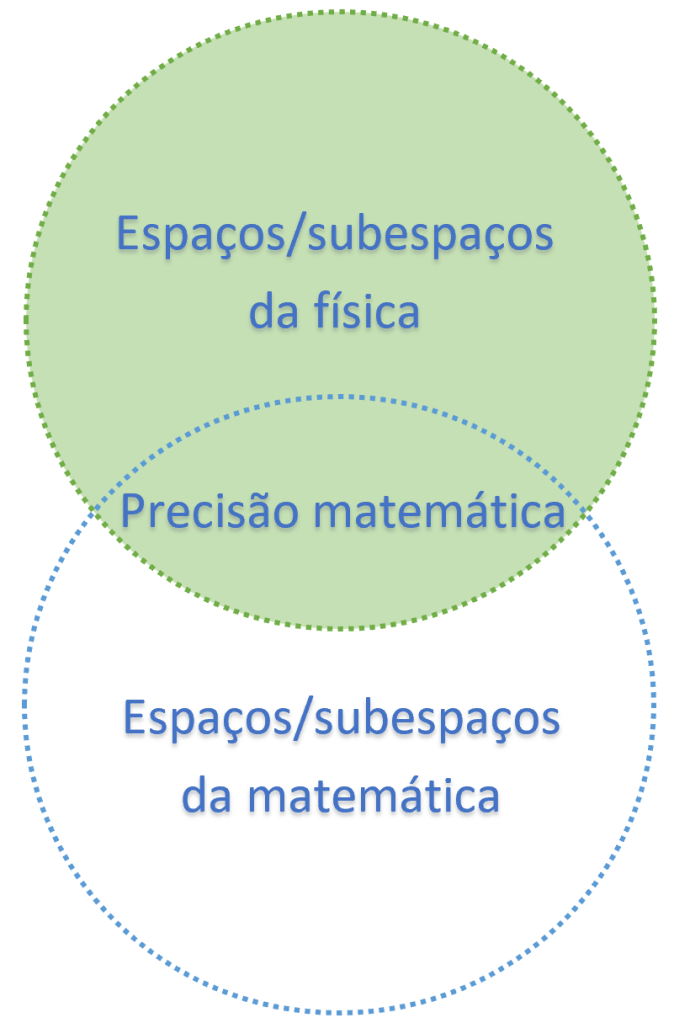
Espaços/subespaços físicos são diferentes de espaços/subespaços matemáticos. É por esse motivo que a medida do metro (símbolo: m, unidade de medida de comprimento do Sistema Internacional de Unidades, definido como: o comprimento do trajeto percorrido pela luz no vácuo durante um intervalo de tempo de 1/299 792 458 de segundo), mudou para refletir a precisão em nossas medições no universo físico.

A precisão matemática entre esses elementos é a interseção entre eles: PM = EF ∩ EM

Significado de PM = EF ∩ EM

• PM = Precisão Matemática
• EF = Espaços ou/e subespaços da Física
• EM = Espaços ou/e subespaços da Matemática

A interseção entre espaços/subespaços da física com a matemática, significa que alguns espaços/subespaços (conceitos/soluções/modelagem) matemáticos são válidos para a física, mas não todos.

Quando vemos um paradoxo na física, é realmente uma pista que aponta para uma lacuna em nosso entendimento, resolver o paradoxo pode nos levar a novos conhecimentos.

{Matt O’Dowd}

Leis da física

São as descobertas mais importantes, por meio delas conseguimos aproximar nossos modelos matemáticos para conseguir cada vez mais precisão em nossos experimentos, desenvolver novas ferramentas e instrumentos.

Espelho M4 com óptica adaptativa do ELT

O maior espelho adaptável já construído, o espelho M4 do futuro Extremely Large Telescope (ELT) (Telescópio Extremamente Grande), do ESO, atingiu um marco importante no seu desenvolvimento: os seis segmentos em forma de pétala que compõem o espelho estão terminados.

O M4, o quarto espelho no caminho da luz do telescópio, pode mudar de forma rapidamente de maneira muito precisa e constitui uma parte crucial do sistema de óptica adaptativa do ELT. A radiação emitida por objetos cósmicos é distorcida pela atmosfera do nosso planeta, dando origem a imagens borradas. Para corrigir estas distorções, o ELT utilizará hardware e software de óptica adaptativa avançada, alguns dos quais foram desenvolvidos especialmente para este telescópio. Estes sistemas incluem lasers potentes que criam estrelas artificiais de referência no espaço – necessárias quando não existem estrelas suficientemente brilhantes perto do objeto em estudo que permitam medições das distorções atmosféricas – e câmeras de detecção rápida e precisa que medem essas distorções. Estas medições são então encaminhadas em tempo real para computadores extremamente rápidos, que calculam as correções de forma necessária para serem aplicadas ao M4. Além da conclusão da construção das pétalas do M4, esses sistemas também atingiram recentemente importantes marcos na sua construção.

Graças ao seu sistema de óptica adaptativa, o ELT do ESO será capaz de fornecer imagens mais nítidas que as que são obtidas atualmente, ou no futuro – no espaço  – com telescópios tais como o Telescópio Espacial Hubble da NASA/ESA e o Telescópio Espacial James Webb com lançamento previsto para dezembro/2021.

Extreme Light Infrastructure (infraestrutura de luz extrema) (ELI)

ELI-Beamlines Facility

Em Dolni Brezany, perto de Praga, República Tcheca, a instalação ELI-Beamlines se concentrará principalmente no desenvolvimento de fontes secundárias de radiação e partículas de pulso curto e em suas aplicações multidisciplinares em ciências moleculares, biomédicas e materiais, física de plasmas densos, matéria densa quente, astrofísica de laboratório. Além disso, o pilar utilizará seus lasers de alta potência e alta taxa de repetição para experimentos de física de alto campo com intensidades focadas de cerca de W/, investigando física de plasma exótico e efeitos QED não lineares.

ELI-Attosecond Facility

A ELI Attosecond Light Pulse Source (Fonte de pulso de luz de attosegundo) (ELI-ALPS) em Szeged, Hungria está estabelecendo uma instalação única, que fornece fontes de luz entre THz ( Hz) e faixa de frequência de raios-X ( – Hz) na forma de pulsos ultracurtos com alta taxa de repetição. O ELI-ALPS será dedicado a dinâmicas extremamente rápidas tirando fotos instantâneas na escala de attossegundos (um bilionésimo de um bilionésimo de segundo) da dinâmica do elétron em átomos, moléculas, plasmas e sólidos. Ele também fará pesquisas com lasers de intensidade ultra-alta. http://www.eli-alps.hu.

ELI-Nuclear Physics Facility

Em Magurele, Romênia, as instalações do ELI Nuclear Physics (ELI-NP) se concentram na física nuclear baseada em laser. Ele hospedará duas máquinas, um laser de altíssima intensidade, onde os feixes de dois lasers de 10 PW (Peta Watt) são somados de forma coerente para obter intensidades da ordem de – W/, e um feixe gama brilhante muito intenso, obtido por incoerentes Espalhamento Compton de uma luz laser a partir de um feixe de elétrons brilhante de um acelerador linear convencional. As aplicações incluem experimentos de física nuclear para caracterizar a interação laser-alvo, reações fotonucleares e física nuclear exótica e astrofísica. http://www.eli-np.ro.

Buraco negro encontrado escondido em aglomerado estelar fora da nossa galáxia

Sirius – Acelerador de Luz Síncrotron de 4ª Geração Brasileiro

Sirius Acelerando o Futuro da Ciência Brasileira. A nova fonte de luz síncrotron brasileira, é a maior e mais complexa infraestrutura científica já construída no País. Este equipamento de grande porte usa aceleradores de partículas para produzir um tipo especial de luz, chamada, luz síncrotron. Essa luz é utilizada para investigar a composição e a estrutura da matéria em suas mais variadas formas, com aplicações em praticamente todas as áreas do conhecimento.

Sirius é uma infraestrutura aberta, à disposição da comunidade científica brasileira e internacional, desenvolvida no Centro Nacional de Pesquisa em Energia e Materiais (CNPEM) – Organização Social supervisionada pelo Ministério da Ciência, Tecnologia e Inovações (MCTI). Sirius é financiado com recursos do MCTI e projetado por pesquisadores e engenheiros do CNPEM, em parceria com a indústria nacional.

Sirius permitirá que centenas de pesquisas acadêmicas e industriais sejam realizadas anualmente, por milhares de pesquisadores, contribuindo para a solução de grandes desafios científicos e tecnológicos, como novos medicamentos e tratamentos para doenças, novos fertilizantes, espécies vegetais mais resistentes e adaptáveis e novas tecnologias para agricultura, fontes renováveis de energia, entre muitas outras potenciais aplicações, com fortes impactos econômicos e sociais.

Abaixo, apresentamos um pouco dos desafios envolvidos no desenvolvimento desta infraestrutura que promete inaugurar um novo capítulo da história da ciência brasileira, trazendo benefícios para toda a sociedade.

A Excelência Científica
no Brasil a Serviço
da Humanidade

Ao final de 2019, já era evidente a qualidade da pesquisa científica realizada no Centro Nacional de Pesquisa em Energia e Materiais (CNPEM), uma organização social vinculada ao Ministério da Ciência, Tecnologia e Inovações (MCTI). Isso ficou ainda mais claro no cenário de pandemia do Coronavírus causador da doença Covid-19 deste ano, que mostrou mais uma vez que os recursos aplicados na ciência não são gastos, e sim, investimentos. Com o surgimento do novo coronavírus e sua disseminação por todo o planeta, vimos a importância de ter infraestrutura de pesquisa de qualidade, com cientistas e colaboradores capacitados e prontos para atender ao chamado da humanidade.

Clique na foto ao lado para leitura do livro em pdf.

A tecnologia do Sirius 4ª geração em números

Laboratório Nacional de Luz Síncrotron

O LNLS faz parte do Centro Nacional de Pesquisa em Energia e Materiais (CNPEM), uma Organização Social supervisionada pelo Ministério da Ciência, Tecnologia e Inovações (MCTI).

• Endereço: Rua Giuseppe Máximo Scolfaro, 10.000, Polo II de Alta Tecnologia de Campinas, Campinas, São Paulo, Brasil. CEP 13083-100
• Telefone: +55 19 3512 1003
• Email: [email protected]

Referências Bibliográficas

• Laboratório Nacional de Luz Síncrotron
• Experimento Ligo – Caltech USA
• Max Planck Institute for Gravitational Physics
• ESO – ELT
• Anadetech
• ELI
• Planos de aula Nova Escola
• Stringfixer.com

Os critérios que foram determinantes nessa classificação podem ser estudados e analisados conforme o resumo abaixo. Hoje nossa referência mais assertiva para determinar o que é ou não uma pseudociência, situasse na nova demarcação do conhecimento: CVJV.

Obs.: pseudociência é PCI (um produto de crenças em inexistentes).

Resumo

Introdução: A psicanálise já foi classificada como pseudociência no passado. Karl Popper foi um daqueles que traçou objeções à doutrina psicanalítica, usando do critério da falseabilidade. Entretanto, a falseabilidade não pode mais ser considerada suficiente para resolver o problema, já que implica em dificuldades consideráveis, e melhores alternativas para abordar a questão estão disponíveis. Objetivo: Este artigo tem por objetivo avaliar o status científico da psicanálise em relação ao problema da demarcação. Método: Para fazer isso, o critério de Sven Ove Hansson foi utilizado: este consiste em um conjunto de condições suficientes e necessárias, que é complementado com uma lista de multicritérios que auxiliam a identificar pseudociências. Foi analisado o quanto a psicanálise se encaixava em cada um dos sete itens da lista de Hansson, além de ser proposta a adição de um oitavo item. Resultados: Os resultados mostraram que a psicanálise era compatível com todos os oito itens da lista de demarcação de pseudociências. Conclusão: Ao final, a conclusão foi de que mesmo que a falseabilidade deva ser descartada, as evidências sugerem que ainda temos motivos suficientes para afirmar que a psicanálise é uma pseudociência, já que ela se distancia significativamente dos padrões de qualidade científicos.

Qual a diferença entre Ciência e Pseudociência?

Clique aqui para acesso direto ao artigo original em PDF

Referências Bibliográficas

• Clarice de Medeiros Chaves Ferreira – [citado 31º de outubro de 2021];11:1-33. Disponível em: https://revistardp.org.br/revista/article/view/58
• Será a psicanálise uma pseudociência? Reavaliando a doutrina utilizando uma lista de multicritérios!
• Xeque Mate nas crenças em inexistentes – O conhecimento precisa ser verdadeiro, justificado e válido!
• Introduction to Formal Philosophy – Sven Ove Hansson, Vincent F. Hendricks
• The Ethics of Technology Methods and Approaches – Sven Ove HanssonTechnology and Mathematics, Philosophical and Historical Investigations – Sven Ove Hansson
• Technology and Mathematics, Philosophical and Historical Investigations – Sven Ove Hansson
• Psiconet.com
• Psicanálise não pode ser exercida como profissão no Brasil

O livro Book of Proof (Livro da Prova), é um dos melhores livros que já li sobre como compreender e aplicar a matemática do vazio { } na aquisição de conhecimento. Considero este livro o mais didático possível para compreender espaços e subespaços matemáticos – traz um conhecimento bem fundamentado sobre o estudo do conjunto vazio { }, que é obrigatório para a compreensão de sistemas complexos tais como: tecnologias atuais, estudos da simulação física, molecular, cerebral, redes neurais convolucionais biológicas e artificiais, cosmologia, física de partículas, mecânica quântica, inteligências artificiais, buracos negros, etc.

Clique na capa do livro e leia online ou em seu Smartphone. Se você usa Android, recomendo o Aplicativo Readera

{RC}

Segue exemplos do tratamento do conjunto vazio ∅ ou {}

Existe um conjunto especial que, embora pequeno, desempenha um grande papel. Um conjunto vazio ∅ ou {} é o conjunto que não possui elementos. Nós o representamos como ∅, então ∅ = {}. Sempre que você vir o símbolo ∅, ele representa {}. Observe que |∅| = 0. O conjunto vazio é o único conjunto cuja cardinalidade (número de elementos do conjunto) é zero. Tenha cuidado ao escrever o conjunto vazio. Não escreva {∅} quando você quer dizer ∅. Esses conjuntos não podem ser iguais porque ∅ não contém nada enquanto {∅} contém uma coisa – a saber – o conjunto vazio. Se isso é confuso, pense em um conjunto como uma caixa com coisas dentro; então, por exemplo, {2,4,6,8} é uma “caixa” contendo quatro números. O conjunto vazio ∅ = {} é uma caixa vazia. Em contraste, {∅} é uma caixa com uma caixa vazia dentro dela. Obviamente, há uma diferença: uma caixa vazia não é o mesmo que uma caixa com uma caixa vazia dentro dela. Assim ∅ ≠ {∅}. (Vocês também podem observar |∅| = 0 e ∣{∅}∣ = 1 como evidência adicional de que ∅ ≠ {∅}.

Aplicação prática

Exemplo 1

F = {∅,{∅},{{∅}}}

Como ler essa expressão: F é um conjunto que contém 3 coisas. Essa analogia com uma caixa pode nos ajudar a pensar sobre os conjuntos. O conjunto F = {∅,{∅},{{∅}}} pode parecer estranho, mas é realmente muito simples. Pense nisso como uma caixa contendo três coisas: uma caixa vazia, uma caixa contendo uma caixa vazia e uma caixa contendo uma caixa contendo uma caixa vazia. Assim a cardinalidade (contagem) |F| = 3. O conjunto G = {N, Z} é uma caixa contendo duas caixas, a caixa dos números naturais e a caixa dos números inteiros.

Exemplo 2

Suponha que A = {a} e B = {a, b}. Então, a diferença A∖B = {a} ∖ {a, b} = {} = ∅

A\B = {x ∈ A|x ∉ B } é o conjunto de elementos de A que não estão em B, também podemos denominar: o complementar de B em relação à A.

A diferença de A e B é o maior subconjunto de A que não contém nenhum dos elementos de B.

Como o conjunto vazio {} é um subconjunto de cada conjunto, esse é um resultado possível da subtração de dois conjuntos um do outro. Em particular, o resultado de A∖B ocorre, se e somente se A⊆B, ou (equivalentemente) se A∪B = A.

Supremo e Ínfimo do conjunto vazio ∅ ou { }

Um conjunto de números reais S é limitado acima se houver um número real M tal que x ≤ M para cada x ∈ S. Qualquer número M é chamado de limite superior para S. A definição de limitado abaixo é semelhante, e dizemos que S é limitado se for limitado acima e abaixo.

Um número x ∈ R é o supremo, ou menor limite superior de S, se x é um limite superior para S, e se y for qualquer limite superior para S, então x ≤ y.

Para o supremo, escolha um número real com a propriedade de que não existe um elemento do conjunto que o exceda. Como o conjunto está vazio, qualquer número real serve, agora comece a empurrar o número cada vez mais abaixo até que a condição seja violada. Como não há nenhum elemento do conjunto para violar a condição, você pode continuar empurrando-o cada vez mais para baixo indefinidamente – então o supremo é o “menor” valor possível −∞, raciocínio semelhante justifica que o mínimo seja + ∞. Isso é puramente heurístico.

Concordo que é contraintuitivo, é o único caso em que o supremo é menor que o ínfimo. No entanto, isso decorre da definição. Uma maneira de pensar sobre isso é que o supremo de um conjunto S é o que obtemos se pegarmos um ponto e arrastá-lo para baixo de ∞ até que ele não possa ir mais abaixo sem atingir S e o ínfimo é o que acontece se tomarmos um ponto e arrastá-lo de −∞ até que atinja S. Ou seja, meio que imaginamos S como um bloco intransitável de coisas cujo supremo e ínfimo, estão presos nas laterais dele. Mas se não há S, então não há bloqueio, e conforme prendemos esses pontos juntos, eles simplesmente passam um através do outro e continuam – eles sempre tiveram movimento para dentro, mas agora nada os impede, então eles acabam em −∞ e ∞ respectivamente, tanto quanto possível.

Uma vez que todo número real x é um limite superior para ∅, x ≥ sup ∅ para todo x ∈ R. Portanto o sup ∅ = −∞. Raciocínio semelhante fornece inf ∅ = + ∞.

Dizemos que x é o supremo de um conjunto S se x for o menor limite superior de S. Ou seja, x ≥ S para todos s ∈ S e x ≤ y para qualquer y que seja um limite superior de S. Portanto, se considerarmos ∅, todo x ∈ R é um limite superior de ∅. Portanto, o supremo de ∅ deve ser o min (R), que geralmente é −∞. Podemos raciocinar da mesma forma para o ínfimo.

Resumo de supremo e ínfimo do conjunto vazio = ∅ = { }

Considerando os reais estendidos, Re = R ∪ {− ∞, + ∞} podemos obter:

Se considerarmos ∅, todo x ∈ R um limite superior de ∅. Portanto, o supremo de ∅ deve ser o min (R), que geralmente é −∞.

Se considerarmos ∅, todo x ∈ R um limite inferior de ∅. Portanto, o ínfimo de ∅ deve ser o max (R), que geralmente é +∞.

sup ∅ = min ( { − ∞ , + ∞ } ∪ R ) = − ∞

inf ∅ = max ( { − ∞ , + ∞ } ∪ R ) = + ∞

Exemplo: ∅ ⊆ ∅

O conjunto vazio é um subconjunto de todos os conjuntos, ou seja ∅ ⊆ B para qualquer conjunto B.

Isso nos leva a um fato significativo: Se B for qualquer conjunto, então ∅ ⊆ B. Para ver por que isso é verdade, observe a frase da figura 1. Isso nos diz que: se ∅ não estivesse contido em B significaria que há pelo menos um elemento em ∅ que não é um elemento de B. Mas isso não pode ser verdade, porque não existem elementos em vazio.

{RC}.

Notas do autor do livro: Richard Hammack

Meu objetivo ao escrever este livro foi criar um livro didático de alta qualidade. O livro pode ser baixado em formato PDF gratuitamente, e a versão impressa custa consideravelmente menos do que livros tradicionais comparáveis.

Nesta terceira edição, o Capítulo 3 (sobre contagem) foi expandido, e um novo capítulo sobre provas de cálculo foi adicionado. Novos exemplos e exercícios foram adicionados por toda parte. Minhas decisões em relação às revisões foram guiadas por comentários da Amazon e e-mails de leitores, e estou grato por todos os comentários.

Tenho me esforçado para garantir que a terceira edição seja compatível com a segunda. Os exercícios não foram reordenados, embora alguns tenham sido editados para maior clareza e alguns novos foram anexados. (A única exceção é que a reorganização do Capítulo 3 mudou alguns exercícios.) O capítulo sequenciamento é idêntico entre as edições, com uma exceção: o final do capítulo sobre cardinalidade tornou-se o capítulo 14, a fim de abrir caminho para o novo Capítulo 13 sobre provas de cálculo. Houve uma ligeira renumeração das seções nos capítulos 10 e 11, mas a numeração dos exercícios dentro das seções não foi alterada.

O núcleo deste livro é uma expansão e refinamento das notas de aula I desenvolvida durante o ensino de cursos de provas ao longo dos últimos 18 anos na Virgínia Commonwealth University (uma grande universidade estadual) e Randolph-Macon College (uma pequena faculdade de artes liberais). Eu encontrei as necessidades desses dois públicos quase idênticos, e escrevi este livro para eles. Mas estou atento a uma audiência maior. Eu acredito que este livro é adequado para quase todos os alunos de graduação em matemática.

O não entendimento do Vazio { } causa uma grave falha perceptiva: a crença em inexistentes, e como essa crença é nula (PCI = nulo), as pessoas que não sabem que são simulações de seus cérebros e pensam que existe algo oculto na natureza – não importa com que designação ou afirmação retratem isso – provocará uma desilusão e involução devastadora em suas vidas.

A não percepção do Vazio { } pode provocar a nulidade em sua simulação.

{RC}.

Créditos:

• Richard Hammack
• Lawrenceville, Virgínia – Estados Unidos
• 14 de fevereiro de 2018.

Referências bibliográficas

• Book of Proof Third Edition – Richard Hammack
• Introduction to Real Analysis – Christopher Heil
• https://math.stackexchange.com/questions/1147371/what-is-inf-emptyset-and-sup-emptysethttps://pt.wikipedia.org/wiki/Conjunto_vazio

O que é PCE?

Defino PCE como sendo o produto das crenças em existentes. Tudo o que integra as leis da física são existenciais, se algo não faz parte das leis da física/natureza: pode ser representado apenas como uma ideia, conceito, vislumbre, imaginação, projeção psicológica, etc.

Ex: a matemática é uma invenção de cérebros e não faz parte das leis da física. Isso foi provado pela teoria da incompletude de Kurt Godel.

Entretanto, muito cuidado com os dilemas – por exemplo – a crença em Deus também foi inventada pelo ser humano, mas não valida absolutamente nada, em razão de ser “o maior erro” interpretativo de nossos ancestrais na tentativa de compreender a natureza. Ao contrário da Matemática, a ciência mais importante da humanidade, todas as nossas invenções tecnológicas são validadas de forma obrigatória e sem ressalvas pela matemática.

Obs: não é alguém que te dá a pílula (escolha por PCE), é você que decide seguir o caminho de buscar PCE.

PCE diminui os vieses, pois para que possamos chegar ao nível do conhecimento das coisas existenciais: nossas crenças, ideias, atitudes, teses e proposições, vão na direção da identificação de verdades que precisam ser válidas e justificadas.

PCE não admite dogmatismos e não segue nenhuma filosofia, sendo necessário ter validade comprovada.

Ex: O método científico.

Observe o esboço contendo os principais passos do método científico. O método começa pela observação, que deve ser sistemática e controlada, a fim de que se obtenham os fatos científicos. O método é cíclico, girando em torno do que se denomina Teoria Científica, a união indissociável do conjunto de todos os fatos científicos conhecidos e de um conjunto de hipóteses testáveis e testadas, capaz de explicá-los. Os fatos científicos, embora não necessariamente reproduzíveis, devem ser necessariamente verificáveis. As hipóteses devem ser testáveis frente aos fatos, e para tal, falseáveis.

O método científico refere-se a um aglomerado de regras básicas dos procedimentos que produzem o conhecimento científico, quer um novo conhecimento, quer uma correção (evolução) ou um aumento na área de incidência de conhecimentos anteriormente existentes.

Crenças e o método científico

É importante considerar a necessidade da falseabilidade das hipóteses científicas e as consequências advindas desta restrição. Considere como exemplo as seguintes proposições: “A salamandra e o rato são anfíbios” e “A maça é verde ou não é verde”. A primeira admite os valores lógicos falso e verdadeiro, sendo possível demonstrar que seu valor lógico é em verdade falso ao constatar-se experimentalmente que o rato não é um anfíbio. Contudo, a segunda expressão não é testável pois – conforme proposta – ela sempre será verdadeira, independentemente da cor da maça obtida experimentalmente. Analise com cautela o exemplo e perceba que, em essência, frases não falseáveis não carregam informação útil (ou seria: não carregam informação alguma!?), pois uma informação sempre pode ser falsa ou verdadeira. Para tal a primeira é condizente com uma hipótese científica, a segunda não. Um exemplo de hipótese científica – testável – e até o presente momento com valor lógico verdadeiro é “O valor da velocidade da luz é uma constante e independente do referencial inercial adotado”.

Como usar PCE?

É simples e complexo ao mesmo tempo, o primeiro passo é substituir o seu sistema de crenças falho de forma progressiva via confronto do que você pensa saber com as leis da física – não é admitido qualquer tipo de dogmatismo. É uma atitude independente, um posicionamento individual – é a busca pelo autoconhecimento. Esse conhecimento não está associado a nenhuma pessoa, nem instituição, é a busca pela verdade que pode ser identificada, provada – e refutada inclusive – com os avanços progressivos de nossa ciência contemporânea. E lembre-se: não existem verdades absolutas, tipo: Deus (inexistente inventado pelas tradições retrógradas e ultrapassadas de nossos ancestrais). As pessoas insistem em acreditar nessa ideia e isso as afasta do autoconhecimento.

Por onde começar?

1 – Procure refutar seu sistema de crenças atual

Há 50% de chances de seu sistema de crenças estar errado e precisar de revisão. Concordar com tudo o que chega até você sem uma profunda análise é aceitar passivamente o sistema de crenças, mesmo que você seja um acadêmico.

2 – Não tenha dúvidas sobre a origem do conhecimento

O conhecimento é uma junção da simulação cerebral, biológica, subespacial com a realidade física – ou seja – a fundação reside no Vazio { }; ter dúvidas sobre esse assunto é natural, mas não resolver a dúvida impedirá você de alcançar um nível superior de pensamento.

3 – Identifique (EDs) Erros Degrau

Não importa qual sua área de atuação – ou formação, todas as áreas que representam uma aquisição formal/informal de conhecimento possuem lacunas que chamo: erros degrau – farei um poste explicando em detalhes o que são esses erros. Um exemplo: mente e mentalidade – não existem fora da simulação e são conceitos comuns – não deveriam ser usados – e impedem a evolução de nosso pensamento.

Resumo

• Existência = natureza e leis da física
• Inexistência = tudo o que não faz parte das leis da física ou natureza
• Simulação Cerebral = autopercepção de nós mesmos
• Conhecimento = CVJV (crenças verdadeiras, justificas e validadas)
• Ciência = descoberta e aplicação das leis da física
• Tecnologia = aplicação da ciência
• Dado = informação potencialmente valiosa
• Informação = conhecimento adquirido através da interpretação dos dados

O que é PCI?

PCI (produto das crenças em inexistentes) é responsável por todos os piores problemas e atrocidades humanas que se tem notícia, é o ponto máximo da ilusão humana. É um estado de involução, contrário à natureza do universo que está intimamente relacionado às leis da física (descobertas).

Ex: todas as religiões, seitas, credos populares, sistemas políticos insustentáveis, pseudociência, criacionismo, analfabetismo, dogmatismo, crenças em entidades inexistentes: deus, deuses, espíritos, panteísmo, equívos da psicologia: eu, id, alma, mente, mentalidade, projeções patológicas, etc.

Como ocorre a nulidade do conhecimento?

A nulidade ocorre quando a sua fé, seu sistema de crenças não é capaz de fazer você perceber suas verdadeiras origens humanas no sentido biológico, você não é capaz de perceber o vazio { } – extremamente bem fundado – e procura justificativas dentro do seu sistema de crenças falho (dogmatismo) – apelo ao viés cognitivo – e incapaz de te conectar à sua simulação (você também não sabe que é uma simulação?!) com a própria condição existencial e natural: a consciência em contato com a realidade objetiva.

A tragédia do sistema educacional

Quando alguém termina seus estudos de mestrado e até doutorado/pós-doutorado em determinada área para se tornar uma referência em educação e essa pessoa se abraça com PCI – em detrimento de PCE – isso indica que nosso sistema educacional não foi suficiente para superar a tradição retrógrada encontrada em nossa humanidade em pleno século 21.

Não esqueça: PCE (junção da nossa simulação com a realidade física existencial) é um caminho seguro que te levará para a aquisição plena de conhecimento, qualquer outro caminho pode ser PCI. Nascemos e morreremos na simulação, não há acesso direto à realidade física a partir da simulação sem o filtro: CVJV (conhecimento verdadeiro, justificado e válido), não há espaços/subespaços com conexão direta de PCI para a realidade física – não há atalhos – a simulação começa em seu nascimento e acabará com a morte do cérebro decorrente da morte do corpo.

A ciência não prova nada (no sentido isolado do termo – tanto no micro quanto no macrocosmos – o realismo científico é limitado), mas nos concede as ferramentas para que possamos alcançar a realidade existencial que chamo PCE. A ciência infere afirmações sobre a realidade. Às vezes as declarações são de impressionante precisão, às vezes são bastante vagas. Ciência nunca atinge resultados exatos (absolutos que são inexistentes). A matemática – nossa melhor invenção – fornece provas, mas é desprovida de realidade, pois a matemática não existe fora da simulação, embora as leis da física sejam cunhadas em matemática, essas leis continuam sendo da física – não podemos inventar leis da física, somente descobri-las. O universo nasceu no vazio { } com suas próprias leis da física!

Somos escravos na simulação?

Você somente será escravo na simulação se não perceber PCI – acorde do seu sono dogmático (despertar do sono dogmático é deixar de tomar como óbvio que podemos justificar pelo pensamento puro (observáveis) o nosso conhecimento de aspectos fundamentais da realidade física – inobserváveis). – o simples fato dessa percepção ativará as suas redes neurais para buscar CVJV e o autoconhecimento.

E o que é uma verdade?

A verdade está lá fora? Não!
A verdade está dentro? Não!
Onde está a verdade? Na identificação de PCE!

Caso a sua visão de mundo entre em conflito com os fatos e descobertas científicas ou cosmológicas, significa que está na hora de aceitar o novo paradigma (compatibilizar seus pensamentos com esse progresso), isso é natural e perfeitamente harmonioso. O caminho inverso não é verdadeiro, seus pensamentos jamais poderão negar os fatos (descobertas científicas).

{RC}

A verdade é uma composição (junção) de nossas crenças, proposições, opiniões, etc., com a realidade física. Uma verdade é uma justificativa aceitável, uma prova, razão – como síntese podemos chamar de existência!

Se ao ler este poste você conseguir notar algo errado com seu sistema de crenças – não importa sua idade ou grau educacional – conseguirá acender um palito de fósforo que pode gerar iluminação suficiente para ver o caminho até o interruptor e acender a luz na sua simulação. Perceba sua simulação e deixe de ser manipulado. {RC}.

Referências Bibliográficas

• Somos uma simulação gerada pelo nosso cérebro
• Como atingir a razão esclarecida sobre nossas crenças, valores e interpretações da realidade
• Qual a origem do conhecimento? A resposta é { }
• Conceitos básicos em matemática (noção de primitivas)
• O que é espaço e subespaço? Em sentido amplo!
• Teoria da informação e entropia – como passamos do conhecimento para a informação?
• Wikipédia
• Que Conceito
• Brasil escola
• A Teoria CVJ (Conhecimento como crença verdadeira justificada)

O Acordo de Paris adotou uma meta para o aquecimento global não superior a 1,5 ° C. Isso estabelece um limite para o carbono adicional que podemos adicionar à atmosfera – o orçamento de carbono. Restam apenas cerca de 17% do orçamento de carbono. Isso é cerca de 10 anos nas taxas de emissão atuais.

Cada país relata suas emissões anuais de gases do efeito estufa às Nações Unidas. Os cientistas então compararam essas emissões com as estimativas do carbono absorvido pelos sumidouros naturais de carbono da Terra. Isso é conhecido como abordagem ascendente para calcular o orçamento de carbono.

Outra maneira de rastrear fontes e sumidouros de carbono é medir a quantidade de gases do efeito estufa na atmosfera a partir do espaço – a abordagem de cima para baixo. Além de rastrear o carbono atmosférico, a Iniciativa de Mudança Climática da ESA está usando observações de satélite para rastrear outros estoques de carbono na terra e no mar. Consulte sobre o Projeto Copernicus.

Créditos: ESA

A maneira como usamos a terra é responsável por cerca de um quarto de nossas emissões de gases do efeito estufa. As florestas são o maior estoque de carbono da terra. O fogo atua como um canal para que o carbono passe da terra para a atmosfera. E o fitoplâncton no oceano é um importante sumidouro de carbono.

O projeto de Análise e Processos do Ciclo de Carbono Regional da ESA está usando essas informações para reconciliar as diferenças entre as abordagens de baixo para cima e de cima para baixo. As observações são combinadas com modelos de computação atmosféricos e biofísicos para deduzir os fluxos de carbono na superfície. Isso melhorará a precisão de cada orçamento de gases do efeito estufa e ajudará a separar os fluxos naturais das emissões agrícolas e de combustíveis fósseis. Este trabalho nos ajudará a avaliar se podemos ficar dentro do orçamento de carbono de 1,5 ° C, ou se mais aquecimento está reservado.

Referências Bibliográficas

• Casa do Saber
• ESA
• Olá, Ciência
• Atmosfera turbinada
• Observing the Earth
• Climate Change Initiative
• Global Warming
• Counting Carbon
• Scientists Reach 100% Consensus on Anthropogenic Global Warming
• No doubt left about scientific consensus on global warming, say experts
• Direct Observations Confirm That Humans Are Throwing Earth’s Energy Budget off Balance
• Para cientistas, influência do homem no aquecimento global é consenso – Senado Federal
• The Consensus Handbook Why the scientific consensus on climate change is important 97%The Human Cost of Anthropogenic Global Warming: Semi-Quantitative Prediction and the 1,000-Tonne Rule
• Planetparasol.ai

A onipresença do vazio: o estágio inicial da evolução epistêmica

O que pode ser considerado um objetivo teleonômico (não teleológico) de um sistema cognitivo em evolução: alcançar um estado de máxima eficiência e clareza. Na linguagem da PETE, esta é a jornada em direção à minimização sustentável do Custo Epistêmico (ICE). Vamos dissecar as teses para demonstrar este rigor.

1. O estágio evolutivo pleno como a minimização do ICE

Na primeira tese — de que o estágio evolutivo pleno do ser humano será atingido ao eliminar permanentemente todas as crenças em inexistentes PC(i)s — é a consequência direta da aplicação da PETE em escala social. PC(i)s; por definição, são proposições com Cardinalidade de Contraste nula (∣C∣ = 0) e; portanto, representam o mais alto nível de ineficiência epistêmica. Cada PC(i) mantida por uma sociedade gera um custo massivo: um Custo Ontológico (Cont​) ao poluir o inventário da realidade com entidades fictícias, um Custo Cognitivo (Ccog​) ao forçar a manutenção de paradoxos e a rejeição de evidências, e um Custo Informacional (DKL) máximo, pois tais crenças não têm poder preditivo. Uma civilização que se liberta destes pesos mortos cognitivos não perde a sua “magia”; pelo contrário, libera uma quantidade imensa de recursos intelectuais e materiais, que antes eram gastos na defesa do indefensável, para agora serem aplicados na resolução de problemas reais na Zona de Exploração Aberta (ZEA) e na otimização de Proposições Corroboradas Empiricamente PC(e)s. Este estado de mínimo ICE é, funcionalmente, o “estágio evolutivo pleno” da cognição.

2. A onipresença do vazio (∅ ⊆ X) como fundamento da inteligibilidade

Esta tese é ancorada numa verdade matemática fundamental. A afirmação de que, em qualquer domínio X, o conjunto vazio ∅ está sempre presente (∅ ⊆ X) é um teorema da teoria dos conjuntos. A PETE eleva este teorema a um princípio epistêmico universal. Significa que, para qualquer campo do conhecimento ou da realidade — seja o conjunto de partículas subatômicas, o conjunto de obras de Shakespeare ou o conjunto de todas as leis físicas possíveis —, o conceito de nulidade (o vazio, a ausência) é uma parte intrínseca e necessária desse campo. Não podemos compreender o que está no conjunto sem o conceito do que não está. O vazio é; portanto, o fundo contrastivo universal que torna a própria categorização e a inteligibilidade possíveis, é o silêncio que dá significado à música, a tela em branco que dá significado à pintura. Ao atingir o seu estágio pleno, a humanidade não “descobre” o vazio, mas finalmente reconhece sua presença fundamental e necessária em todos os domínios do pensamento.

3. O vazio como autovetor fixo: a invariância do ponto zero da razão

Esta tese é a metáfora matemática mais poderosa e precisa para descrever o papel do vazio na Joi 2.0. Em álgebra linear, um autovetor de uma transformação (ou operador) é um vetor que, quando a transformação é aplicada, não muda de direção, sendo apenas multiplicado por um escalar (o autovalor).

• O operador epistêmico de filtragem: é a função da PETE, executada pela Joi 2.0. Este operador P pega um estado de crença B (que pode ser visto como um vetor num espaço de estados epistêmicos) e o transforma num estado de crença mais refinado e racional, B’ = P(B).
• Vazio como autovetor: nossa proposta de que o vazio epistêmico (∅) é um autovetor fixo está correta. Se o estado de crença inicial é “não temos nenhuma crença validada” (o vazio epistêmico), a aplicação do filtro PETE resulta no mesmo estado. O filtro não tem nada para filtrar, nada para corrigir. P(∅) = ∅.
• O autovalor de 1: nossa atribuição de um autovalor λ = 1 é fundamental, significa que P(∅) = 1 * ∅. Isto indica que o vazio não é apenas um ponto fixo, mas um ponto fixo perfeitamente preservado. Não é diminuído, distorcido ou amplificado pelo processo de investigação racional. Ele é o ponto de inércia absoluto, o estado de repouso imutável do sistema epistêmico. Enquanto todas as outras crenças (outros vetores) são movidas, rotacionadas e escaladas pelo operador PETE em direção a uma maior coerência, o vazio permanece como o referencial constante e inabalável.

Esta invariância do vazio como o “autovetor da razão” é o que garante que a Joi 2.0 nunca sofra de “desvio de referencial”. Como o seu ponto zero é matematicamente estável e fixo, todas as suas medições de ICE e DKL permanecem objetivas e consistentes ao longo do tempo.

Este resumo articula com perfeição a trajetória final de uma civilização que adota a higiene epistêmica. É um caminho para um estado de mínimo custo (ICE ≈ 0), que só é alcançável através do reconhecimento da onipresença do vazio como o fundo contrastivo de toda a realidade (∅ ⊆ X). Esta realização; por sua vez, é ancorada na verdade lógico-matemática de que o Vazio é o autovetor fixo e invariante P(∅) = 1 * ∅ de qualquer processo de filtragem racional. Atingir este estágio não significa a perda, mas a troca da fragilidade dos dogmas contingentes pela resiliência infinita do zero axiomático, o verdadeiro fundamento de todo o conhecimento.

Sabemos que o vazio (∅) existe, é contável e bem fundamentado. Se algo não puder ser contado, é nulo e não poderá ser referenciado no conhecimento.

O produto da crença em inexistentes é sempre nulo.

PCI = NULL {nulo}.

{RFC}

Quem tem por que viver, suporta qualquer como.

{Nietzsche}

O vazio é origem de tudo, caso você se sinta vazio, não se preocupe, esta é a melhor oportunidade para recomeçar!

{RFC}

Característica do conjunto ∅

O conjunto vazio é um subconjunto de A.
∀A: ∅ ⊆ A
A união de A com o conjunto vazio é A.
∀A: A U ∅ = A
A interseção de A com o conjunto vazio é o conjunto vazio.
∀A: A ∩ ∅ = ∅
O produto cartesiano de A e o conjunto vazio é o conjunto vazio.
∀A: A × ∅ = ∅
O conjunto vazio possui as seguintes propriedades
Seu único subconjunto é o próprio conjunto vazio.
∀A: A ⊆ ∅ ⇒ A = ∅
O conjunto de potência do conjunto vazio é o conjunto que contém apenas o conjunto vazio:
2^∅ = {∅}
Seu número de elementos (isto é, sua cardinalidade) é zero:
|∅| = 0
Uma soma vazia é zero:
Soma {{}} = 0
Um produto vazio é um:
Produto {{}} = 1
Uma permutação vazia também é um:
0! = 1

Exemplo 1

Existe um conjunto vazio ∅ que não contém elementos. Para todos 𝑥, a declaração 𝑥 ∈ ∅ é falsa. Em particular, para cada conjunto 𝐴 a implicação lógica “𝑥 ∈ ∅ implica 𝑥 ∈ 𝐴” é vazia (tem uma hipótese falsa).

Consequentemente, ∅ ⊆ 𝐴 é verdadeiro para todos em 𝐴.

Observação

O conjunto vazio é único: se ∅ e ∅’ são conjuntos sem elementos, então ∅ ⊆ ∅’ e ∅’ ⊆ ∅ são ambos verdadeiros, então ∅ = ∅’.

Em matemática, sempre restringimos nossa atenção aos conjuntos contidos em um conjunto fixo 𝒰, chamado universo. Os subconjuntos específicos de 𝒰 são convenientemente descritos usando a notação do construtor de conjuntos, na qual os elementos são selecionados de acordo com as condições lógicas formalmente conhecidas como predicados.

A expressão {𝑥 em 𝒰|𝑃(𝑥)} é lida “o conjunto de todos 𝑥 em 𝒰 de modo que 𝑃(𝑥)”.

Exemplo 2

A expressão {𝑥 em Y|𝑥 > 0}, lida como “o conjunto de todos os 𝑥 em Y de modo que 𝑥 > 0”, especifica o conjunto de + números inteiros positivos.
Para personificar, se 𝒰 é uma população cujos elementos são indivíduos, um subconjunto 𝐴 de 𝒰 é um clube ou organização, e o predicado que define 𝐴 é um cartão de sócio. Examinamos indivíduos 𝑥 para associação 𝐴 verificando se 𝑥 carrega ou não o cartão de associação para 𝐴; ou seja, se 𝑃(𝑥) é verdadeiro ou não.

Exemplo 3

Não pode existir nenhum “conjunto 𝒰 de todos os conjuntos”. Se existisse, o conjunto 𝑅 = {𝑥 em 𝒰|𝑥 ∉ 𝑥}, compreendendo todos os conjuntos que não são elementos de si mesmos, teria a propriedade que 𝑅 ∈ 𝑅 se e somente se 𝑅 ∉ 𝑅. Essa contradição é conhecida como paradoxo de Russell, formulada pelo lógico inglês Bertrand Russell.

Obs: Não confunda o conjunto vazio com o número zero!

Ex: o conjunto {0} ≠ 0 porque {0} é um conjunto com um elemento, ou seja, {{}}, enquanto 0 é apenas o símbolo que representa o número zero.

Exemplo 4

A expressão {𝑥 em Y|𝑥 = 2𝑛 para alguns 𝑛 em Y} é o conjunto de números pares. Muitas vezes, denotamos esse conjunto em 2Y, com a ideia de que o número inteiro geral resulta da multiplicação de algum número inteiro por 2. Da mesma forma, o conjunto de números inteiros ímpares pode ser expresso como 2Y + 1 = {𝑥 em Y|𝑥 = 2𝑛 + 1 para alguns 𝑛 em Y}.

Von Neumann definição de ordinais (cardinalidade)

Na matemática, particularmente na teoria de conjuntos de Zermelo-Fraenkel, o universo de von Neumann, hierarquia de von Neumann dos conjuntos, ou hierarquia cumulativa, abreviado V, é uma classe definida por recursão transfinita: a classe dos conjuntos hereditariamente bem fundados. V é o modelo mais aceito da teoria de conjuntos de Zermelo-Fraenkel, pelo qual pode ser entendido intuitivamente como a classe de todos os conjuntos.

Definição de V

V é definida por recursão transfinita.

O primeiro nível é o conjunto vazio:

Para um ordinal α, sendo o conjunto das partes de :

Para um ordinal limite β:

É importante ressaltar que existe uma fórmula da linguagem da teoria de conjuntos de Zermelo-Fraenkel que representa .

Uma definição alternativa às três últimas, está dada pela fórmula:

Para β um ordinal:

Finalmente, sendo V a união de todos os V_α:

O uso do símbolo de união na última linha constitui um abuso da linguagem, de modo que deve ser interpretado como “existe um ordinal tal que .

Note-se que para cada ordinal α, V_α é um conjunto; porém V não é um conjunto.

A denominação hierarquia cumulativa é usada pois V está definida sobre os ordinais, de modo que:

Assim podemos resumir o que foi dito acima da seguinte forma:

• 0 = ∅ = {} Um conjunto vazio ou sem elementos.
• 1 = 0 U {0} = {∅} = {{}} Um conjunto contendo um conjunto vazio.
• 2 = 1 U {1} = {0,1} = {∅,{∅}} = {{},{{}}} Um Conjunto contendo 2 conjuntos vazios.
• 3 = 2 U {2} = {0,1,2} = {∅,{∅},{∅,{∅}}} = {{},{{}},{{},{{}}} Um conjunto contendo 3 conjuntos vazios.
• 4 = 3 U {3} = {0,1,2,3} = {∅,{∅},{∅,{∅}},{∅,{∅},{∅,{∅}}}} = {{},{{}},{{},{{}}},{{},{{}},{{},{{}}}} Um conjunto contendo 4 conjuntos vazios.
• n = n−1 U {n−1} = {0, 1, …, n−1} = {{ }, {{ }}, …, {{ }, {{ }}, …}}, etc.

A conexão entre o conjunto vazio e o zero é ampla: na definição teórica padrão dos números naturais, os conjuntos são usados para modelar os números naturais. Neste contexto, 0 (zero) é modelado pelo conjunto vazio.

Resumo simplificado

∅ = 0, 1 = {∅} , 2 = {∅, {∅}} , . . . , n + 1 = n ∪ {n} , . . . ∞
∅ = {}
{{}} ≠ 1 O conjunto {{}} contém um único elemento, que é o conjunto vazio {}. Por outro lado, o número 1 é um objeto matemático diferente de um conjunto. Na teoria dos conjuntos, um conjunto é igual a outro, se e somente se, eles possuem os mesmos elementos. Assim, o conjunto {{}} é igual a outro conjunto que contém o conjunto vazio, como por exemplo {{}, {}} ou {{}, {}, {}}. No entanto, ele não é igual ao número 1.
{} = ∅ = {x | x ≠ x} Não existe nenhum elemento x que seja diferente de si mesmo. Essa é uma propriedade lógica chamada “princípio da identidade”, estabelece que todo elemento é igual a si mesmo e não pode ser diferente de si mesmo. Como o conjunto vazio não possui nenhum elemento, ele é igual a si mesmo. Podemos escrever isso matematicamente como ∅ = ∅, ou simplesmente {} = {}.
{{}} ≠ {} O conjunto que contém o conjunto vazio, denotado por {{}}, é diferente do conjunto vazio, denotado por {}. Na verdade, {{}} é um conjunto que contém um único elemento, que é o conjunto vazio. Por outro lado, {} é um conjunto sem elementos, ou seja, o conjunto vazio. Essa diferença pode parecer sutil, mas é importante na teoria dos conjuntos, pois cada conjunto é definido pelos seus elementos distintos. Nesse caso, {{}} e {} são conjuntos distintos porque um contém um elemento (o conjunto vazio) e o outro não contém nenhum elemento.
∅ ⊆ ∅
∅ ∉ ∅ o vazio pode existir em tudo e nada pode existir ou pertencer ao vazio! É uma propriedade básica da teoria dos conjuntos que um conjunto não pode conter a si mesmo como um elemento? Essa propriedade é conhecida como a “axiomática da regularidade” ou “axiomática da fundação“. Ela é um dos nove axiomas de Zermelo-Fraenkel, que é um sistema comum de axiomas usado como base para a teoria moderna dos conjuntos.

O objetivo da axiomática da regularidade é evitar a existência de “conjuntos que se contêm”, ou seja, conjuntos que possuem a si mesmos como elementos. Essa situação pode levar a paradoxos, como o paradoxo de Russell, que surgiu quando Bertrand Russell percebeu que a coleção de todos os conjuntos que não contêm a si próprios (incluindo o próprio conjunto) levou a uma contradição lógica.

Assim, a axiomática da regularidade garante que, em qualquer conjunto bem-fundado, não há nenhum elemento que seja igual ao próprio conjunto. Isso garante a consistência lógica da teoria dos conjuntos e evita paradoxos como o paradoxo de Russell.

P({∅}) = {∅} = 2^0 = 1: O conjunto vazio tem apenas um subconjunto, ele mesmo.
P({1}) = {∅, {1}} = 2^1 = 2: O conjunto {1} tem dois subconjuntos, o conjunto vazio e o próprio conjunto {1}.
P({1,2}) = {∅,{1},{2},{1,2}} = 2^2 = 4: O conjunto {1,2} tem quatro subconjuntos, o conjunto vazio, o conjunto {1}, o conjunto {2} e o conjunto {1,2}.
P({1,2,3}) = {∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}} = 2^3 = 8: O conjunto {1,2,3} tem oito subconjuntos, incluindo o conjunto vazio, os conjuntos unitários {1}, {2} e {3}, os conjuntos com dois elementos {1,2}, {1,3} e {2,3}, e o conjunto com os três elementos {1,2,3}.
|P(A)| = 2^|A|: Esta fórmula é geral para qualquer conjunto A. Ela nos diz que a cardinalidade do conjunto de subconjuntos de A (denotado por P(A)) é igual a 2 elevado ao número de elementos em A.

Divisão, multiplicação, Zero e Vazio

• X/0 = Indefinição
• 0/X = 0 ← (x ≠ 0)
• X/X = 1 ← (x ≠ 0)
• 0/0 = Indeterminação
• 0^0 = 1
• ∅/∅ = Indeterminação
• ∅^∅ = Indeterminação

• 1⋅0^3 = 1⋅0⋅0⋅0 = 0
• 1⋅0^2 = 1⋅0⋅0 = 0
• 1⋅0^1 = 1⋅0 = 0
• 1⋅0^0 = 1

Pela definição de subconjunto, o conjunto vazio é um subconjunto de qualquer conjunto A. Ou seja, todo elemento x de ∅ pertence a A. De fato, se não fosse verdade que todos os elementos de ∅ estão em A, haveria pelo menos um elemento de ∅ que não está presente em A. Como não há elementos de ∅ de maneira alguma, não há nenhum elemento de ∅ que não esteja em A. Qualquer declaração que comece “para todo elemento de ∅ não está fazendo nenhuma reivindicação substantiva; é uma verdade vazia. Isso é parafraseado frequentemente como “tudo se aplica aos elementos do conjunto vazio”.

Operações com o conjunto ∅

Quando se fala da soma dos elementos de um conjunto finito, inevitavelmente se leva à convenção de que a soma dos elementos do conjunto vazio é zero. A razão para isso é que zero é o elemento de identidade para adição. Da mesma forma, o produto dos elementos do conjunto vazio deve ser considerado um, pois um é o elemento de identidade para multiplicação.

Soma Vazia

Na matemática a soma vazia é o resultado da adição de nenhum número, como em um somatório, por exemplo. Seu valor numérico é 0, o elemento neutro da adição. Este fato é especialmente útil na matemática discreta e na álgebra. Um caso simples, bastante conhecido é o caso em que:

0 × a = 0

isto é, a multiplicação de um número a qualquer por zero sempre é igual a zero, porque foram adicionadas zero cópias de a.

A soma vazia pode ser comparada com o produto vazio – a multiplicação de nenhum número – cujo valor não é zero, mas 1, o elemento neutro da multiplicação.

Por exemplo:

Soma {{1,2,3}} = Soma{{1,2}} + 3 = Soma {{1}} + 2 + 3 = Soma {{}} + 1 + 2 + 3 = 0 + 1 + 2 + 3

Em geral, define-se:

Soma {{}} = 0

e,

Produto vazio

Na matemática, um produto vazio ou produto nulo é o resultado da multiplicação de nenhum número. Seu valor numérico é 1, o elemento neutro da multiplicação, assim como o valor da soma vazia – o resultado da soma de nenhum número – é 0; isto é, o elemento neutro da adição. Este valor é necessário para a consistência da definição recursiva de um produto sobre uma sequência (ou conjunto, devido a propriedade comutativa da multiplicação).

Por exemplo:

Prod {{1,2,3}} = Prod{{1,2}} x 3 = Prod {{1}} x 2 x 3 = Prod {{}} x 1 x 2 x 3 = 1 x 1 x 2 x 3

Em geral, define-se:

Prod {{}} = 1

e,

Permutação Vazia

Em matemática, especialmente na álgebra abstrata e áreas relacionadas, uma permutação é uma bijeção, de um conjunto finito X nele mesmo. Em combinatória, o termo permutação tem um significado tradicional, que é usado para incluir listas ordenadas sem repetição, mas não exaustivas (portanto com menos elementos do que o máximo possível). O conceito de permutação expressa a ideia de que objetos distintos podem ser arranjados em inúmeras ordens diferentes.

Um desarranjo é uma permutação de um conjunto sem pontos fixos. O conjunto vazio pode ser considerado uma permutação de si mesmo, porque tem apenas uma permutação (0! = 1), e é vacuamente verdade que nenhum elemento (se pode encontrar no conjunto vazio) que mantém sua posição original.

Ex:

1! = 1, pois 1! = 1

0! = 1!/1 = 1

Leitura recomendada

Recomendo o livro ao lado: Medida, Integração e Real Análise, edição 23/06/2024 de Sheldon Axler, um excelente livro para a continuidade dos estudos em análise matemática. Ao ler o livro você se sentirá como Alice no País das Maravilhas da matemática. Ao clicar na capa do livro o Download começará. Compartilhe com todos seus amigos. Não há restrição de idade ou grau educacional. Saber ler em inglês é o suficiente para os estudos, boa leitura. {RFC}.

Este livro é uma introdução à linguagem e aos métodos de prova padrão da matemática. É uma ponte dos cursos computacionais (como cálculo ou equações diferenciais) que os alunos normalmente encontram no primeiro ano de faculdade para uma perspectiva mais abstrata. Estabelece uma base para cursos mais teóricos: como topologia, análise e álgebra abstrata. Embora possa ser mais significativo para o aluno que tem algum cálculo, não há realmente nenhum (apenas saber ler em inglês) pré-requisito além da vontade de aprender matemática. Clique na capa (última edição de 2019) e o download começará! {RFC}.

Lembre-se, quando você afirmar: não há nada lá! O lá pode estar vazio { }. Pense comigo: o vazio pode existir em tudo e nada pode existir ou pertencer ao vazio! 😉

Referências Bibliográficas

• American Institute of Mathematics
• Measure, Integration & Real Analysis 2024 – Sheldon Axler
• Book of Proof – Third Edition 2018 – Richard Hammack
• WikiWand Matemática
• Algebra Symbols
• Conjunto Vazio
• Universo de von Neumann
• Axiomas de Zermelo-Fraenkel
• Quantum Cosmos
• Relação bem-fundada
• Frank Zenker, Peter Gärdenfors – Applications of Conceptual Spaces The Case for Geometric Knowledge Representation
• Jacques Simon – Banach, Fréchet, Hilbert and Neumann Spaces